【研究成果・プレスリリース】熱平衡化の問題は、一般的な形では解決不可能な問題であることを証明

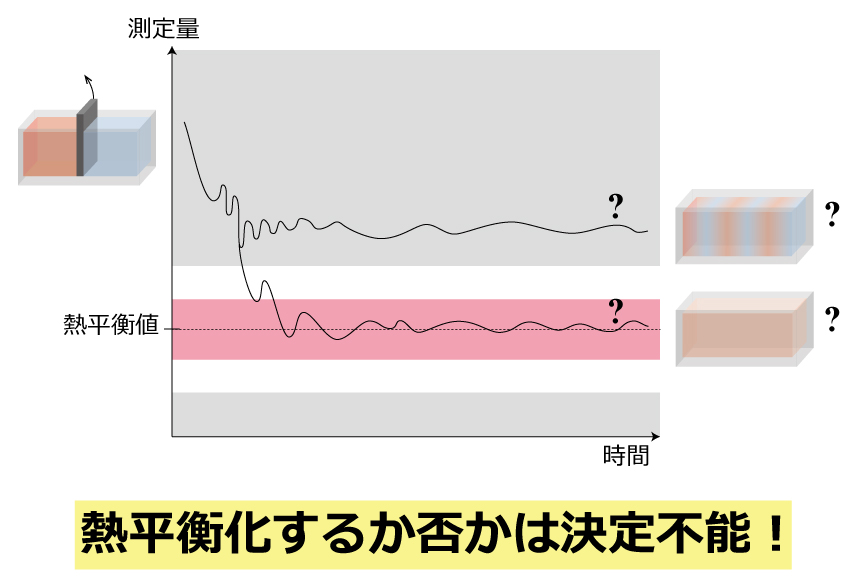
図1：時間がたったときに熱平衡化するか（ピンクの領域）、熱平衡化しないか（グレーの領域）、は決定不能。

【概要】
左側を熱して高温に、右側を冷やして低温にした物体を用意し、その物体を放置すると、最終的には一様な温度の熱平衡状態に緩和します。これは熱平衡化と呼ばれる現象です。ほとんどすべての物体は熱平衡化しますが、一部の物体は熱平衡化しないことも知られています。どういう物体は熱平衡化するのか、という問題は、多くの研究者が取り組んできた未解決問題でした。本研究では、過去のほとんどの研究がしてきたように、「与えられた物体は熱平衡化するか」という問題に直接取り組むのではなく、「そもそも熱平衡化の問題は解決可能なのか」という真逆の問いを立て、これを物理学と理論計算機科学の手法を融合させた全く新しいアプローチで解析しました。その結果、驚くべきことに、「与えられた物体は熱平衡化するか」という問題は、一般的な形では解くことができない、決定不能な問題であることが数学的に証明されました。そのため、例えば物体の熱平衡化の有無を決める一般的な定理は原理的に存在しえないことが厳密に示されました。この結果は、熱平衡化現象について「人類が決して知りえないこと」の存在を明らかにしています。

【背景】
真ん中に仕切り板のある容器の左側に熱水を、右側に冷水を入れて仕切り板を外して放置すると、十分時間がたった後には温度が一様なぬるま湯になります。このぬるま湯の温度は、最初の熱水と冷水の持つエネルギーから決まる平衡状態の温度です。このような過程を熱平衡化現象と呼びます。ほとんどすべての物体は熱平衡化しますが、熱平衡化しない物体も存在することが知られています。熱平衡化しない物体の場合、測定している量が平衡状態の値とは異なる値に緩和します（図1）。熱平衡化が生じることは、熱力学や統計力学といった現代の物理学の土台が成り立つための必要条件でもあるため、熱平衡化は物理学における重要な研究対象です。しかし、多くの研究者の試行錯誤にもかかわらず、与えられた物体が熱平衡化するか否かを判定する一般的な方法は見つかっていませんでした。

【手法】
これまでの熱平衡化の研究は、それ以外のほとんどの物理学の研究と同様に、いろいろな物体の熱平衡化の状況をつぶさに観察、解析して、その一般的な性質を明らかにしようとしてきました。しかし、今回の研究は、従来の物理学とは全く異なるアプローチを用いています。今回の研究では、「そもそも熱平衡化の問題は一般的な形で解決しうるのか」というこれまでとは真逆の問題設定をして、これを理論計算機科学（コンピュータが原理的に何が出来るかの数学的証明を行う分野）という全く異なる分野の枠組を導入して解析しました。

特に今回の研究では、「決定可能／不能」という性質に注目しました。どのような出題例が与えられてもそれを解く方法が存在する場合、その問題は決定可能です。逆にそのような方法が存在しない場合、その問題は決定不能です。例えば素数判定問題は、どんな数が与えられてもそれが素数か否かを正しく判定する方法が存在するので、これは決定可能な問題です。決定不能な問題の代表例としては「停止問題」が挙げられます。この問題は、与えられたプログラムに従ってコンピュータを動かしたときに、コンピュータが「いつか停止する」のか「停止せず永遠に動き続ける」のかを答える問題です。停止問題は、計算機科学者アラン・チューリング（注1）によって、決定不能であることが証明されています。

（注1）：アラン・チューリング
計算機科学の基礎を築いたイギリスの計算機科学者（1912-1954）。第二次大戦時にナチスドイツの暗号エニグマの解読に携わったことでも知られています。2021年6月から発効されたイギリスの新50ポンド紙幣の肖像画にも選ばれています。

【研究結果】
熱平衡化の有無という問題を、決定可能／不能という観点から解析したところ、それは決定不能であることを証明することが出来ました。すなわち、どのような物体と測定量の組に対しても、それが熱平衡化するか否かを正しく判定する一般的方法や基準、定理は決して存在しないということです。これは物理学者の努力が足りないためではなく、そのようなものはそもそも原理的に存在しえないのです。これは量子多体系の物理学と理論計算機科学の融合によって実現された、従来の物理学とは違う新しいタイプの研究成果です。

今回の証明ではまず、熱平衡化現象が実はコンピュータと同等以上の計算能力を有していることを証明します。つまり、コンピュータで出来るどんな計算でも、熱平衡化現象は（広い意味で）計算出来てしまうということです。それを利用して、上述の停止問題を熱平衡化ダイナミクスの中で模倣します。特に、「熱平衡化するか否か」と「コンピュータが停止するか否か」を巧妙に対応させ、コンピュータが停止した場合、そしてその場合に限って熱平衡化が起こるような物体が存在することを示しました（図2）。停止問題は決定不能なので、熱平衡化の有無も決定不能であることが示されます。

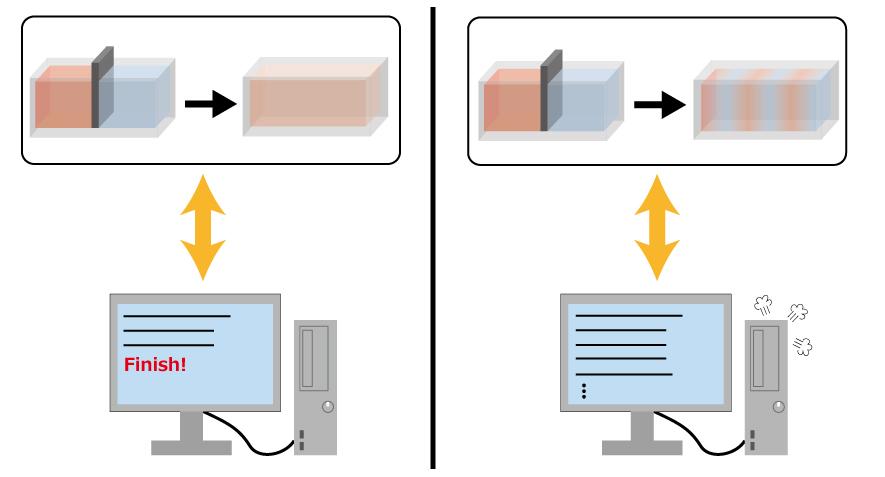
図2：コンピュータが停止する場合（図左）に限って熱平衡化が生じ、コンピュータが停止しない場合（図右）には熱平衡化が生じない。

【今後の期待】
本研究結果は、熱平衡化を判定する一般的方法が存在しないという否定的な側面だけでなく、熱平衡化現象はコンピュータが可能などんな計算や数学的課題でも解くことが出来るという肯定的な側面も有しています。この事実は、熱平衡化現象が従来の想像以上に複雑な現象であること、熱平衡化と数学の間には予想外のつながりがあることを示唆しています。例えば、数学の有名な未解決問題にリーマン予想（注2）がありますが、これに対応して、リーマン予想が偽である場合、そしてその場合に限って熱平衡化するような物体が存在することも示せます。

上記の例に限らず、物理学と理論計算機科学を横断するようなアプローチは、従来の物理学では発見できないような全く新しい成果を見つけ出す可能性に満ちています。本研究成果は、その先駆けの一つとなるものでしょう。

（注2）：リーマン予想
リーマン予想は、数学者ベルンハルト・リーマン（1826-1866）によって提起された、素数の分布の性質に関する予想です。これはクレイ数学研究所が出している7つのミレニアム懸賞問題にも含まれる未解決問題です。