【研究成果】単調でない従属関係のための固有振動接合関数

2024.03.26

単調でない従属関係のための固有振動接合関数

ポイント

固有振動接合関数により単調でない従属関係を表せることを示しました。

研究の概要

2つの変数について、一方の変数が増えるほど、他方の変数が常に増える（あるいは減る）、という単調な従属関係が成り立たない場合があります。単調でない従属関係を表す、ある接合関数^※1を取り上げ、固有振動接合関数^※2と名付けました。分析例として、戦後欧州諸国の内閣について、成立のしやすさと成立から崩壊までの時間を同時に分析した先行研究を取り上げ、そこに固有振動接合関数を導入すると分析が改善できることを示しました。

本研究成果は2024年2月13日に国際学術誌「Political Analysis」のオンライン版に掲載されました。本研究は、科学研究費補助金(19H00584)ならびに学習院大学計算機センターから資金援助を受けています。本発表は、学習院大学グランドデザイン 2039「国際学術誌論文掲載補助事業」より掲載費を助成されています。

発表内容

研究の背景と経緯

2つの変数の関係のうち、各変数の周辺分布に関わらない部分は、接合関数と呼ばれるもので表現できます。2つの変数について、一方の変数が増えるほど、他方の変数が常に増える（あるいは減る）、という単調な従属関係が成り立たない場合があります。しかし、単調でない従属関係を表す接合関数は、あまりよく知られていませんでした。2015年に公刊した接合関数を用いた論文につながる研究の過程で、単調でない従属関係を持つ接合関数の必要性を感じ、今回報告した固有振動関数を導出しました。

研究の内容

単調でない従属関係を表す、ある接合関数を取り上げ、固有振動接合関数と名付けました。図1は、何通りかの固有振動接合関数の密度を等高線と濃淡で表したものです。分析例として、戦後欧州諸国の内閣について、成立のしやすさと成立から崩壊までの時間を同時に分析した先行研究を取り上げ、そこに固有振動接合関数を導入することで、モデルの適合度が高まり、パラメータの推定値の標準誤差が小さくなることを示しました。図2(a)と図2(b)は、各点が内閣を（黒丸が崩壊にまで至ったもの、×印が崩壊に至る前に観察が打ち切られたもの）、横軸が成立のしやすさを、縦軸が成立から崩壊（もしくは観察が打ち切り）までの時間を、それぞれ表します。等高線と濃淡は、図2(a)が正規接合関数を、図2(b)が固有振動接合関数を、それぞれ表します。

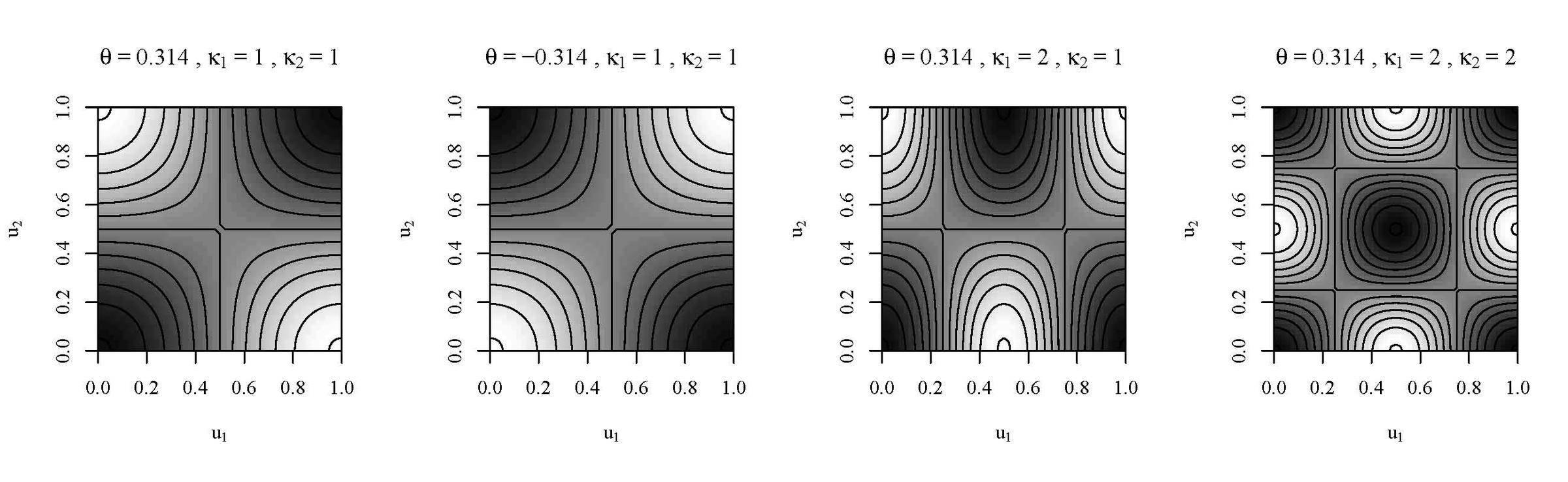
図1

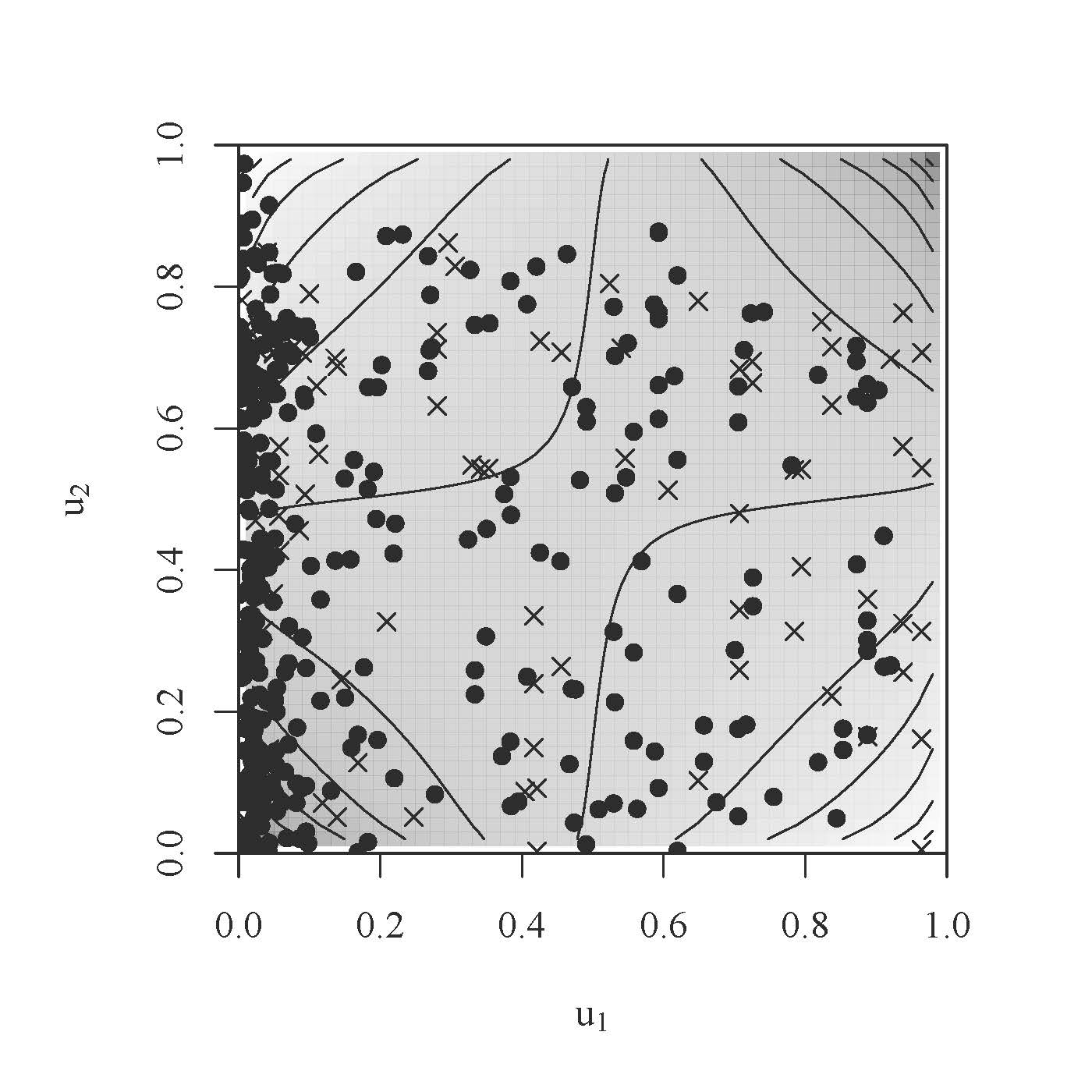
図1(a)

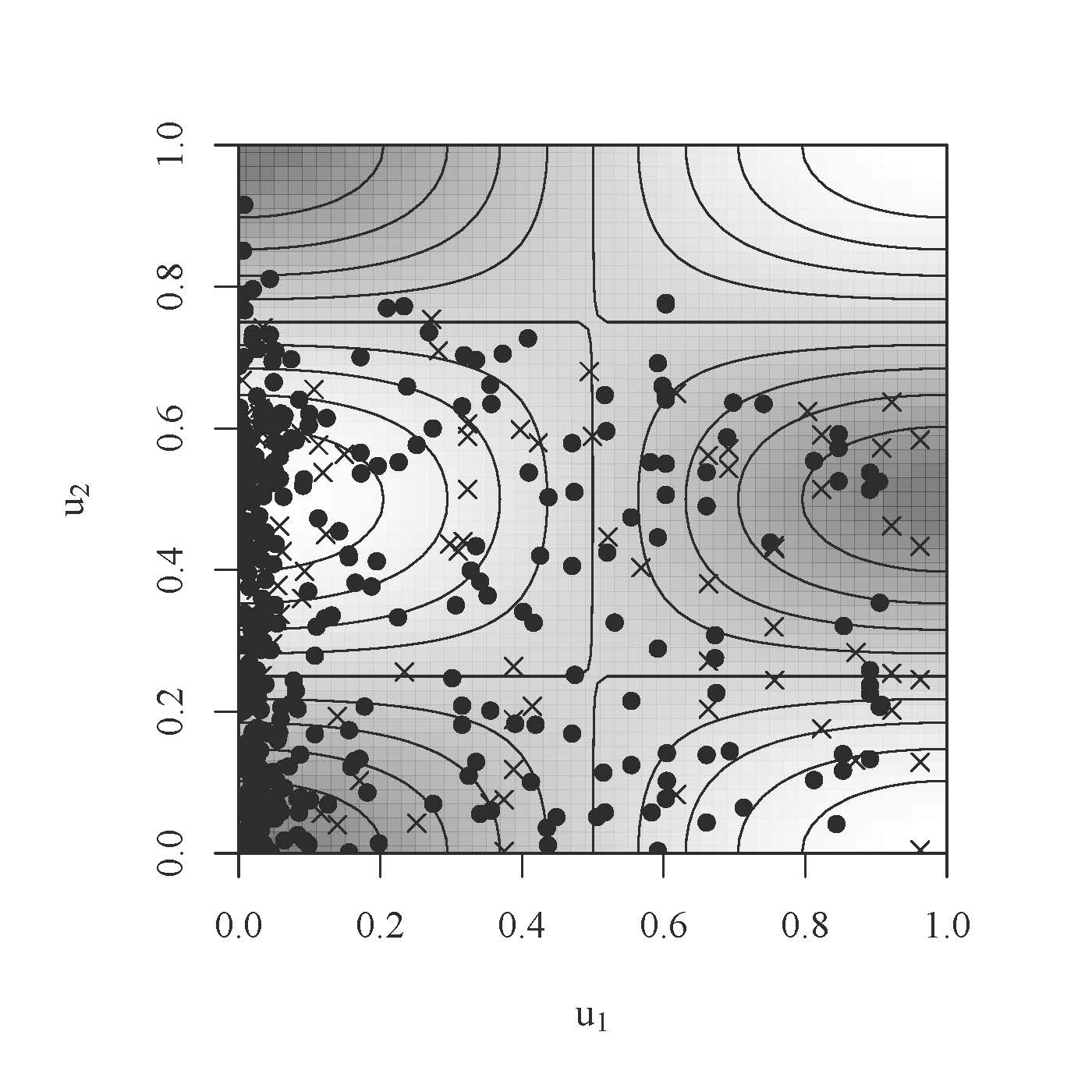
図1(b)

今後の展開

今回は主として2変量の場合を扱ったため、多変量の場合の検討を進めます。また、固有振動接合関数の応用例も増やしていきたいと考えています。

用語解説

※1 接合関数

2つの変数の関係のうち、各変数の周辺分布に関わらない部分を表現できる、ある種の関数。

※2 固有振動接合関数

三角関数を用いた、ある種の接合関数。

論文情報

論文名：Normal Mode Copulas for Nonmonotonic Dependence

雑誌名：Political Analysis

著者名：Fukumoto Kentaro

DOI：10.1017/pan.2023.45

発表者

福元健太郎　学習院大学法学部・教授